不等式 不等式問題[2006年筑波大前期理系第２問]
問題(2006年筑波大前期理系第２問)\(a \ge b \gt 0, x \ge 0\) とし、\(n\)は自然数とする。次の不等式を示せ。(1) \(\displaystyle 0 \le e^x-(1+x) \le \frac{x^2...
不等式 代数 行列の割り算はこうなっている！
行列の計算を習って最初に面食らうのは、交換の法則です。そして、行列計算において最初に立ちはだかる壁は、行列の割り算についてです。結論からいうと、行列にも割り算を考える事はできます。しかし、普通の数と比べて扱いがとてもシビアです。
猫野の微分積分 積分にでてくる∫やdxの記号の意味
積分の式は、\(\displaystyle \int（xの関数）dx\)という形で書かれます。この\(\int\)と\(dx\)の記号は慣れないとなかなか読み解けないものです。記号の意味や解釈はいろいろありますが、ここでは初心者向けに記号の...
猫野の微分積分 超難問√tan(x)の不定積分と定積分の解き方
関数\(\sqrt{\tan(x)}\)の積分です。微分と比較にならないほど積分ははるかに難しいです。まずは、素敵なウルフラムの計算結果を参照してください。わずか数秒でこのような計算をしてしまうWolframAlphaに敬意を表します。Wo...
無限 超実数のイメージがわくように説明するよ
超実数(Hyperreal Number)について調べていると、超フィルターの説明があってそこに入り込んだまま抜け出せず、結局超実数がなんなのかわかったようなわからない状態になります。そこで、超実数についての概略を超簡単に説明します。概略と...
解析 数列の「自明な収束」と「自明でない収束」
数列の収束には、自明な収束と、そうでない収束（狭義の収束）の２種類があります。これらは明確に区別されますが、どちらもひとくくりに収束と呼ばれるため、場合によっては混乱する場合があります。
猫野の微分積分 関数√tan(x)を微分するとこうなる
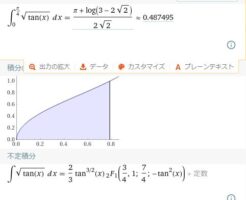
関数\(\sqrt{\tan(x)}\)の微分です。関数\(\sqrt{\tan(x)}\)の微分(導関数)\(\sqrt{\tan(x)}\)の微分は、\(\sqrt{f(x)}\)の微分公式を使って計算します。
数学 数学のお兄さんで知られている横山さんが作ったクイズ本の効果
数学の本「文系もハマる数学」の著者として知られている「数学のお兄さん(横山明日希)」さんが新しい数学クイズの本を作りました。
集合論 集合の集合っていったいどんな集合？
集合って簡単そうで難しい概念です。理由はいろいろ考えられますが、そんな難しいことではなく、ここでは「集合の集合」という用語を具体的例を通して説明したいと思います。集合の例まずは、集合の例をあげます。集合は、中括弧つまり、「｛」と「｝」で囲ん...
数論 数学でびっくりマーク！は階乗記号になります
数学で、５！のように、数字の後ろに！（びっくりマーク）がつくことがあります。これは、数学では階乗記号（かいじょうきごう）と呼ばれています。数学での！は、びっくりマークと言うこともしばしばありますが、エクスクラメーション（マーク/記号）や感嘆...