 統計
統計 メジアンとモードと平均
メジアン(median) 中央値メジアンとは中央値のことで、データを小さい順(もしくは大きい順)に並べ替えて、データ列の真ん中になる値のことです。データが複数個ある場合は、中央値が2つになるので、その中央値の平均をメジアンとします。例){1...
 統計
統計  無限
無限  代数
代数  無限
無限  無限
無限  無限
無限 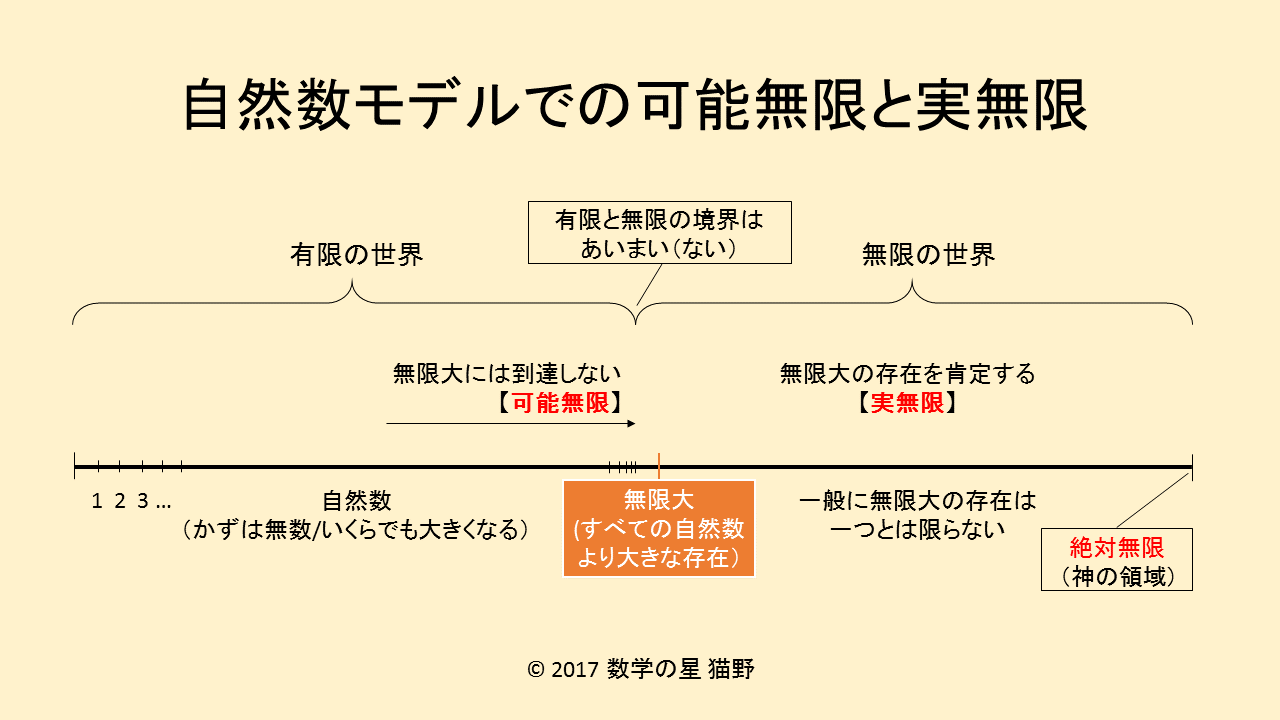 数論
数論  数論
数論  無限
無限  無限
無限