 代数
代数 可算濃度よりも小さい濃度に挑戦
可算濃度と連続濃度Sを可算濃度ℵ0の無限集合とし、その冪集合を2Sとすると、2Sは連続の濃度ℵ1の無限集合である。これについては、調べれば豊富な説明があり、説明しだすとくどくなるのでここでは詳しく述べない。ここで確認しておきたい要点は、「可...
 代数
代数  無限
無限  無限
無限  無限
無限 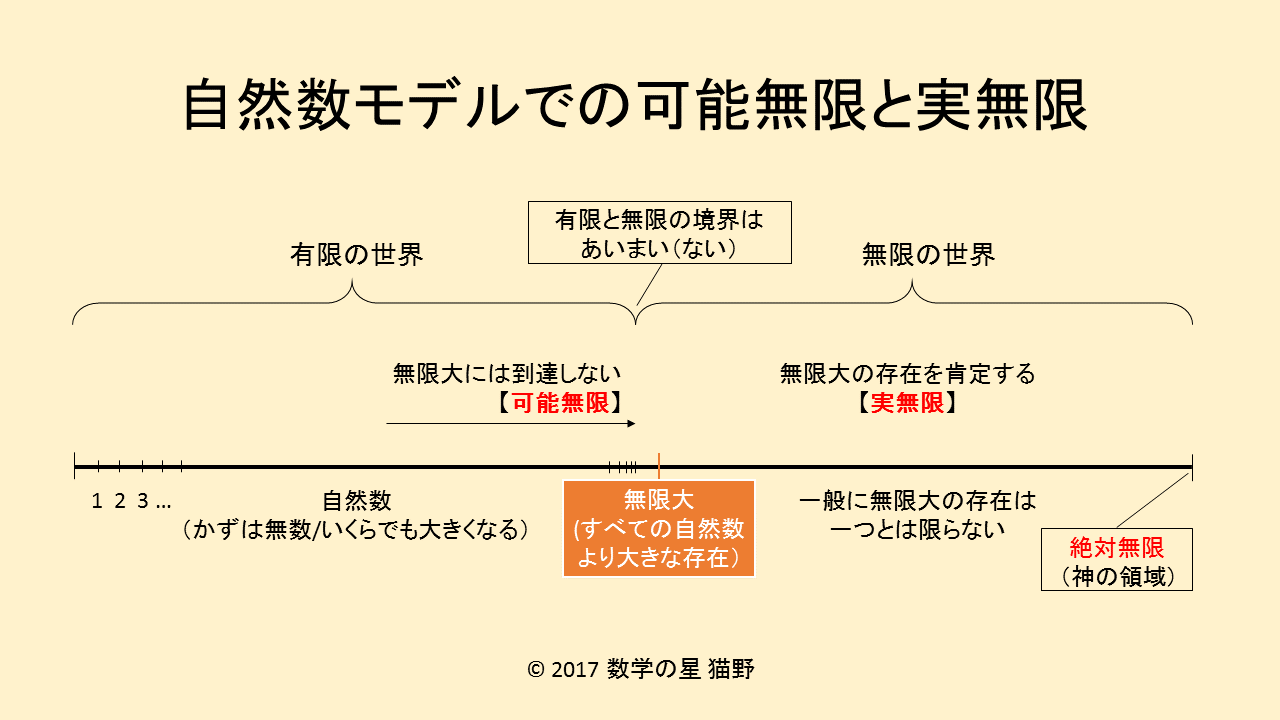 数論
数論  無限
無限  無限
無限  不等式
不等式  無限
無限  無限
無限